[1]   Yotam Dikstein: Oppenheim’s Trickling Down Theorem, 2019. Lecture notes from the Error-Correcting Codes and High-Dimensional Expansion Boot Camp at Simons Institute for the Theory of Computing, Available at https://simons.berkeley.edu/sites/default/files/docs/14119/ecctalkii.pdf.

[2]   Howard Garland: p-adic curvature and the cohomology of discrete subgroups of p-adic groups. Ann. Math., 97(3):375–423, 1973. [doi:10.2307/1970829]

[3]   Alexander J. Hahn and O. Timothy O’Meara: The Classical Groups and K-Theory. Springer, 1989. [doi:10.1007/978-3-662-13152-7]

[4]   Tali Kaufman and Izhar Oppenheim: High dimensional expanders and coset geometries. Europ. J. Combinat., 111(103696), 2023. Preliminary version in STOC’18. [doi:10.1016/j.ejc.2023.103696, arXiv:1710.05304]

[5]   Alexander Lubotzky, Ralph Phillips, and Peter Sarnak: Ramanujan graphs. Combinatorica, 8(3):261–277, 1988. Preliminary version in STOC’86. [doi:10.1007/BF02126799]

[6]   Alexander Lubotzky, Beth Samuels, and Uzi Vishne: Explicit constructions of Ramanujan complexes of type 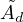. Europ. J. Combinat., 26(6):965–993, 2005. [doi:10.1016/j.ejc.2004.06.007, arXiv:math/0406217]

[7]   Alexander Lubotzky, Beth Samuels, and Uzi Vishne: Ramanujan complexes of type 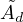. Israel J. Math., 149(1):267–299, 2005. [doi:10.1007/BF02772543, arXiv:math/0406208]

[8]   Grigorii Aleksandrovich Margulis (Григорий Александрович Маргулис): Явные теоретико-групповые конструкции комбинаторных схем и их применения в построении расширителей и концентраторов (Russian) [Explicit group-theoretical constructions of combinatorial schemes and their application to the design of expanders and concentrators]. Problemy Peredachi Informatsii, 24(1):51–60, 1988. Available at https://www.mathnet.ru/eng/ppi686, (English translation in Problems Inform. Transmission, 24(1):39–46, 1988).

[9]   Ryan O’Donnell and Kevin Pratt: High-dimensional expanders from Chevalley groups. In Proc. 37th Comput. Complexity Conf. (CCC’22), pp. 18:1–26. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2022. [doi:10.4230/LIPIcs.CCC.2022.18, arXiv:2203.03705]

[10]   Izhar Oppenheim: Local spectral expansion approach to high dimensional expanders Part I: Descent of spectral gaps. Discr. Comput. Geom., 59(2):293–330, 2018. [doi:10.1007/s00454-017-9948-x, arXiv:1709.04431]

[11]   Omer Reingold, Salil Vadhan, and Avi Wigderson: Entropy waves, the zig-zag graph product, and new constant-degree expanders. Ann. Math., 155(1):157–187, 2005. Preliminary version in FOCS’00. [doi:10.2307/3062153, arXiv:math.CO/0406038, ECCC:TR01-018]

[12]   Alireza Sarveniazi: Explicit construction of a Ramanujan (n₁,n₂,…,n_d-1) -regular hypergraph. Duke Math. J., 136(1):141–171, 2007. [doi:10.1215/S0012-7094-07-13913-9]